Acting with Tables for Solving Puzzles
Acting with tables is also at the center of the various kinds of “thinking-type” puzzles Alexandra has been doing since her early childhood, puzzles that present people with a complex problem and a set of clues for solving it. Among Alexandra’s favorites are those that involve using a table or multiple tables, which she refers to as “grids,” to work toward a solution.
Since Alexandra has been attending college, her mother has included a couple of assorted puzzle books in the care packages she mails each month. According to Alexandra, “Every time I get a book of mixed thinking-type puzzles, I will go through and I’ll find all of the ones that look like this [the ones with the tables] and I’ll do the ones I like. I especially like the ones with the grids. Just, I think it’s more organized. And sometimes I’ve drawn my own grids for these.” In addition to the book of puzzles she keeps in her dorm room, Alexandra also carries one in her backpack so that she can work on them during spare moments throughout the day.
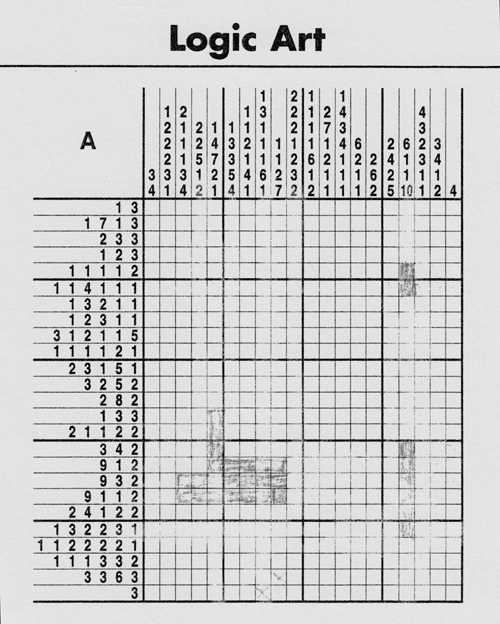
The earliest of these puzzles Alexandra recalls doing are the logic art puzzles, like the sample one she provided from her book (see Figure 13 at right), she has been doing since age seven. Solving these types of puzzles involves using the numerical clues arrayed along each axis to determine which of the cells to blacken and which to leave blank, and in what order, within each column and row. Determining exactly which cells to blacken in involves working reflexively from column to row, much like determining the correct words in a crossword puzzle. When correctly solved, the combination of blackened and blank cells form a simple picture (e.g., a dog, a flower, a baseball mitt). The initial versions of these she encountered in her childhood were briefer, shorter versions of the one offered here. As Alexandra stated, “We had a computer game, actually, that had a simpler format, like normally it was just one box’s worth, like there aren’t even ones that easy in this book.”
For the last seven years, among her favorites are complex word puzzles (see Figure 14 at right). According to Alexandra, she first encountered these word puzzles in a book her younger sister had been given as part of her ACT preparation program. As Alexandra stated, her sister’s teacher “had these logic puzzle books that she gave her students. And I saw one and went ‘give it to me.’” Since that initial encounter, Alexandra indicated that has regularly engaged with these puzzles, sometimes doing several a week and at other times only doing one or two. She estimates that she has done “way over 100” of these kinds of puzzles over just the past few years.
In this brief video clip (below) from one of our interviews, Alexandra demonstrates and discusses how she works to solve the word puzzle pictured above.
At this point in the interview, Alexandra is working to figure out which items Brian and Jeff requested and in what order. In the video, Alexandra describes working to solve the puzzle by re-representing information provided in the numbered clues located toward the top of the page as x’s and dots in the table on the left of the page she refers to as the “grid.” For clues indicating that two factors do not match, such as the one indicating that “Brian is not party invitations,” Alexandra places an x in the cell at the intersection of the column for “Brian” and the row for “party.” For clues indicating that two factors do match, such as the one indicating that “Jeff’s item is ordered first,” she places a dot in the cell at the intersection of the column for “Jeff” and the row for “first.” Alexandra modified the labels of two of the rows in the grid from “requested” to “ordered” and from “retrieved” to “picked up” in order to make them consistent with the language used in the clues.
After initially filling in as many x’s and dots as she can, Alexandra then works reflexively among the clues, the notes she has made to herself, and the x’s and dots of the grid to fill in any additional cells she can. She then re-represents the dots in the grid as words in the appropriate cells of the table she refers to as the “chart” at the right of the page, which she has modified in the same way as the grid. In essence, Alexandra is “reading” the dots at the intersections of columns and rows and re-representing them as names, items, and sequences in the chart. Ultimately, the words in the “chart” indicate the answers to the puzzle questions about who ordered which item and in what sequence those orders were placed and picked up. As Alexandra indicates in the video, arriving at the answers to all the questions is a matter of working reflexively among “the grid and the notes, and the, the chart.”
The tables Alexandra acts with in solving these puzzles allow her to view and order the information and clues provided to her in ways that afford logical deduction. In this sense, the tables function as what Lynch (1988) defined as “revelatory objects,” representations which select from, simplify, and order an object of study, and, at the same time, analyze what they reveal (p. 154). The tables accomplish a number of other functions revealed by the tables she acts with for her engineering engagements. Tables represent complex information in an economical fashion. The x’s, dots, and blank cells of the “grid” and the filled and blank cells of the “chart” serve to remind Alexandra of what she already knows and help her determine what information she needs to look for as she returns to the information provided in the clues and the notes she has jotted. The x’s and dots of the grid and the filled cells of the chart also visually represent when the puzzle has been solved. In integrating prose and visual representations, the tables of the word puzzle also allow Alexandra to coordinate multiple semiotic media. The same is true of the logic art puzzle, which integrates numeric and visual representations.